Huffman Code
Published:
This is my personal notes for Huffman Code.
Introduction
Huffman coding is an efficient method of compressing data without losing information. In computer science, information is encoded as bits—1’s and 0’s. Strings of bits encode the information that tells a computer which instructions to carry out. Video games, photographs, movies, and more are encoded as strings of bits in a computer. Computers execute billions of instructions per second,and a single video game can be billions of bits of data. It is easy to see why efficient and unambiguous information encoding is a topic of interest in computer science.
Information Encoding
In information theory, the goal is usually to transmit information in the fewest bits possible in such a way that each encoding is unambiguous. For example, to encode A, B, C, and D in the “fewest” bits possible, each letter could be encoded as “1”. However, with this encoding, the message “1111” could mean “ABCD” or “AAAA”—it is ambiguous.
Encodings can either be “fixed-length” or “variable-length”(Huffman Code).
Fixed-length encoding
A fixed-length encoding is where the encoding for each symbol has the same number of bits. For example:
Below is a valid answer, but it is inefficient since there exists a shorter (and still unambiguous) encoding of these letters.
| A | 0000 |
| B | 0101 |
| C | 1010 |
| D | 1111 |
Actually, ABCD can be encoded as follows:
| A | 00 |
| B | 01 |
| C | 10 |
| D | 11 |
How many bits are needed to represent n different symbols (using fixed-length encoding)?
To represent n symbols with a fixed-length encoding, log2(n) bits are needed. Because each bit has two possible values: 1 or 0. Therefore, with log2(n) bits, n different symbols can be represented.
Variable-length encoding (Huffman Code)
In variable-length encoding, we consider the frequence of different symbols, the idea is that symbols that are used more frequently should be shorter while symbols that appear more rarely can be longer. This way, the number of bits it takes to encode a given message will be shorter, on average, than if a fixed-length code was used. In messages that include many rare symbols, the string produced by variable-length encoding may be longer than one produced by a fixed-length encoding.
Imagine that a appears 10000 times, but b,c,d,e,f,g,h,…z appears 1 time. In a fixed-length encoding, we use log2(26) bits for each symbol. But actually, we could use only 1 bit for a, log2(25)+1 for other symbols. This is the core idea of Huffman Code.
Huffman Coding Algorithm
The Huffman Coding Algorithm always select 2 symbols with smallest freq, construct a subtree with these 2 leaves, the freq of root node is the sum of these 2 leaves. Add the new freq to the original freq list, select 2 symbols with smallest freq again…. until there is only 1 freq left. (which should be 1 is freq is represented as 0-1)
Take a list of symbols and their probabilities.
Select two symbols with the “lowest” probabilities (if multiple symbols have the same probability, select two arbitrarily).
Create a binary tree out of these two symbols, labeling one branch with a “1” and the other with a “0”. It doesn’t matter which side you label 1 or 0 as long as the labeling is consistent throughout the problem (e.g. the left side should always be 1 and the right side should always be 0, or the left side should always be 0 and the right side should always be 1).
Add the probabilities of the two symbols to get the probability of the new subtree.
Remove the symbols from the list and add the subtree to the list.
Go back through the list and take the two symbols/subtrees with the smallest probabilities and combine those into a new subtree. Remove the original symbols/subtrees from the list, and add the new subtree to the list.
Repeat until all of the elements are combined.
Example:
| Symbol | A | B | C | D | E |
| Freq | 0.6 | 0.1 | 0.1 | 0.1 | 0.1 |
Corresponding Huffman Tree
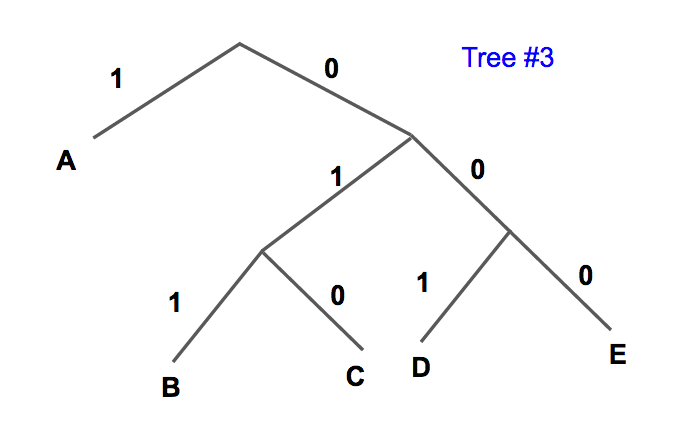
Corresponding Huffman Code
| Symbol | A | B | C | D | E |
| Code | 1 | 011 | 010 | 001 | 000 |
Note: 1 and 0 could be exchanged, it can be assigned as you like.
